今日の話もあまり,弁護士っぽい話はでてこない。
ただ,こういう日常を暮らしている,埼玉の一弁護士がいるのだなと思って読んでもらえればと思う。
先日,マイナスにマイナスを掛けるとプラスになるということが,姪が理解しにくいので,わかりやすく説明できないかと言われた。
マイナスにマイナスを掛けるとプラスになるなんて,言われてみれば,ちょっと浪漫を感じると,文学的な思いを馳せながら,姪への説明の仕方を考えてみた。
数が数直線上に表わされるという理由は,さておき,とりあえず数直線を使って説明するのがわかりやすいなと思って,次のように考えた。
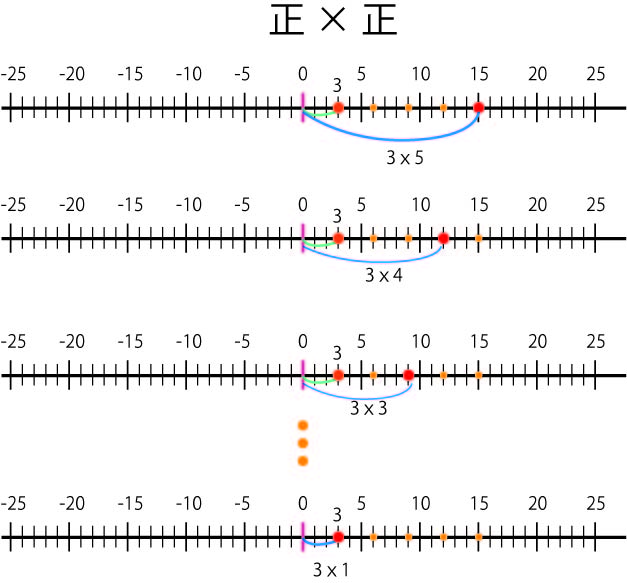
1 正の整数×正の整数
3×5は,3が5個分である。
数直線で,これを説明すると,3×5は,3という数字を,右方向(0から見た3と同じ方向)に5個分のばしたところという意味と考えられる。
同じく,3×4は,3という数字を,右方向(0から見た3と同じ方向)に4個分のばしたところ,3×1は,3という数字を,右方向(0から見た3と同じ方向)に1個分のばしたところという意味と考えられる。
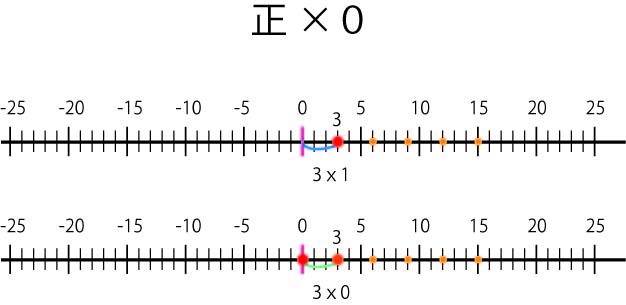
2 正の整数×0
では,3×0はどう考えたらいいか?
まず,3×5=15,3×4=12,・・・・3×1=3というように,掛ける数が1つずつ小さくなると,3ずつ減少していることから,3×0=0だと推測される。
そして,数直線で説明すると,3×0は3という数字を,右方向(0から見た3と同じ方向)に0個分のばしたところという意味と考えられる。これは,自然な考えに思える。
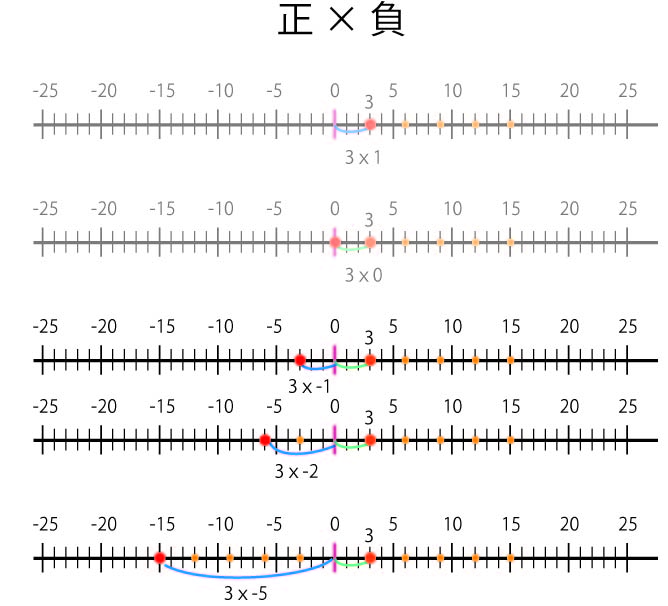
3 正の整数×負の整数
さらに,3×-1はどう考えたらいいか?
3×0より,さらに3減少するはずなので,3×-1=-3だと推測される。
数直線で説明すると,3×-1は3という数字を,右方向(0から見た3と同じ方向)に-1個分のばしたところという意味と考えられる。
言い換えると,3という数字を,左方向(0から見た3と逆の方向)に1個分のばしたところという意味と考えられる。
同様に,3×-2は-6で,3という数字を,左方向(0から見た3と逆の方向)に2個分のばしたところ,3×-5は-15で,3という数字を,左方向(0から見た3と逆の方向)に5個分のばしたところ,という意味と考えられる。
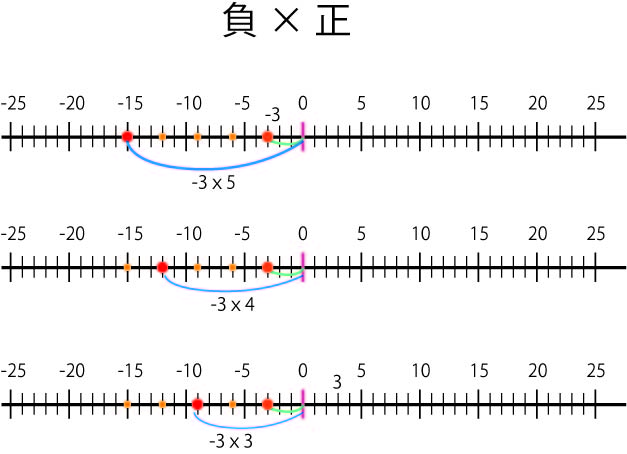
4 負の整数×正の整数
-3×5は,-3が5個分である。-3を5回足せばいいので,-15だろうと推測できる。
数直線で,これを説明すると,-3×5は,-3という数字を,左方向(0から見た-3と同じ方向)に5個分のばしたところという意味と考えられる。
同じく,-3×4は,-3という数字を,左方向に(0から見た-3と同じ方向)に4個分のばしたところ,-3×1は,-3という数字を,左方向に(0から見た3と同じ方向)に1個分のばしたところという意味と考えられる。
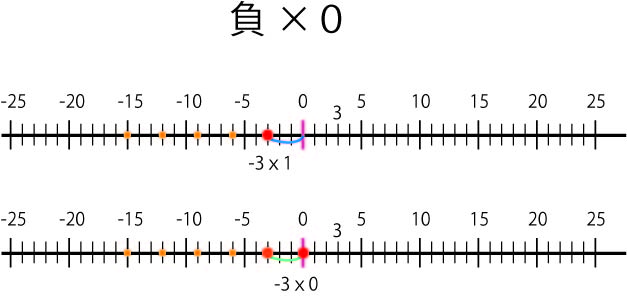
5 負の整数×0
-3×0はどう考えたらいいか?
まず,-3×5=-15,-3×4=-12,・・・・-3×1=-3というように,掛ける数が1つずつ小さくなると,3ずつ増加していることから,-3×0=0だと推測される。
そして,数直線で説明すると,-3×0は-3という数字を,左方向(0から見た-3と同じ方向)に0個分のばしたところという意味と考えられる。これは,自然な考えに思える。
6 負の整数×負の整数
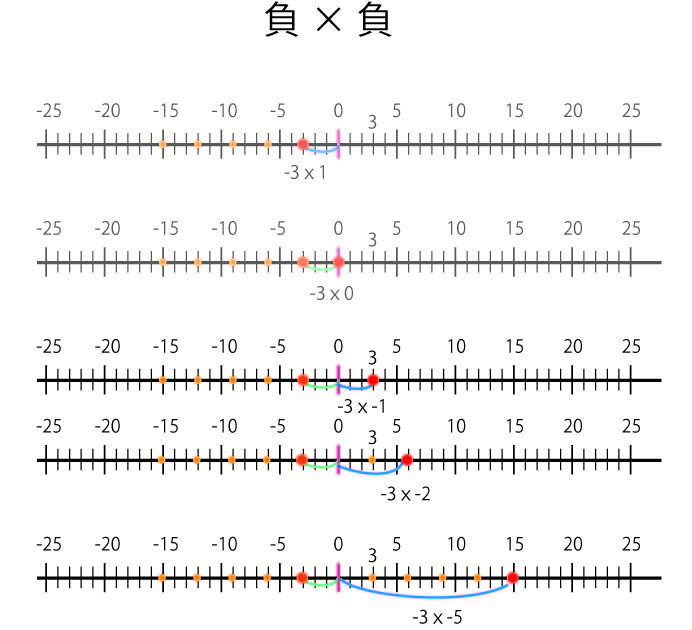
いよいよマイナスにマイナスを掛ける。
-3×-1はどうなるか?
-3×0より,さらに3増加するはずなので,-3×-1=3だと推測される。
数直線で説明すると,-3×-1は-3という数字を,左方向(0から見た-3と同じ方向)に-1個分のばしたところという意味と考えられる。
言い換えると,-3という数字を,右方向(0から見た-3と逆の方向)に1個分のばしたところという意味と考えられる。
同様に,-3×-2は6で,3という数字を,右方向(0から見た-3と逆の方向)に2個分のばしたところ,-3×-5は15で,-3という数字を,右方向(0から見た-3と逆の方向)に5個分のばしたところ,という意味と考えられる。
やはり,マイナスにマイナスを掛けると右方向,プラスになるのである。
わかってもらえたかはわからず
姪には,この説明の仕方でわかってくれたか,まだ聞いていない。
ただ,よく考え出すと,当たり前だと思っていたことが,本当にそうなんだろうかと疑わしくも思えてくる。
例えば,数直線を使って説明したが,数が数直線上の点と対になっているということは,そもそも前提にして良かったのだろうかと思ったりした。もっとも,私は,弁護士であって,数学を追求する立場ではないので,これ以上,深入りしないようにしたい。
アナロジー的な考え方
ともかく,負と負のかけ算を考えるにあたり,推測をしたり,類推したりするというのは,とても数学っぽい思考回路である。こういうのをアナロジーというのだろうか。記憶力や言語能力が低かった私が,唯一得意だった能力が,この思考方法だったと思う。数学や物理は,このアナロジー的な考えさえあれば,たいてい乗り切れる。
見方を変えると,既存のモノから,抽象化して本質的なモノを取り出して,これをさらに今までにないモノに応用して,新しいモノを作り出す思考方法である(正×正,正×0から,正×負,負×正,負×負などを作り出す。)
たとえば,アナロジーな考え方ができれば,小学生でも,次のような問題も解くことができる。
問い
例えば,2を2回掛けるのを2の2乗といい(2×2=4),2を3回掛けるのを2の3乗という(2×2×2=8)。
では,81の0.25乗を求めなさい。
解答
(2の3乗)の4乗=(2×2×2)×(2×2×2)×(2×2×2)×(2×2×2)=2の12乗
ということは,(XのY乗)のZ乗=Zの(Y×Z)乗と推測できる
81の(0.25乗×4)=81の1乗=81であるから
(81の0.25乗)×(81の0.25乗)×(81の0.25乗)×(81の0.25乗)=81
よって,(81の0.25乗)=3
・そういえば-3も解答ですね(虚数は,考えないでね)。
日頃,数学と法律の一致しているところ,相違しているところを考えたりする。20代前半にはじめて法律を勉強しはじめたとき,想像以上に,法律がロジカルではないことに戸惑ったことを思い出した。
アナロジー的な思考方法が,今の弁護士ライフに役に立っていると願いたい。
(了)
